Диффузия носителей заряда

Если по какой-то причине концентрация n носителей заряда в полупроводнике неоднородна, то возникает градиент концентрации носителей:

, м^-4,

где  - векторный оператор (набла); i, j, k – единичные векторы вдоль направлений осей x, y, z декартовой системы координат.

Наличие градиента концентрации приводит к диффузии- движению носителей заряда из области с большей концентрацией в область с меньшей концентрацией, приводящее к выравниванию концентрации носителей заряда по полупроводнику.

Диффузия не связана с электрическим зарядом свободных носителей. Она наблюдается и для нейтральных частиц, например, молекул газа или атомов в твердых телах при нагреве их до достаточно высокой температуры.

В одномерном случае плотность потока частиц при диффузии выражается первым законом Фика:

, м^-2с^-1,                                        (3.20)

где D, м²/c – коэффициент диффузии частицы; знак «минус» указывает на то, что частицы движутся из области с большей концентрацией в область с меньшей концентрацией.

В случае, если диффундирующие частицы заряжены, то возникает диффузионный электрический ток. Диффузионный ток электронов

, А/м²,                  (3.21а)

где D_n – коэффициент диффузии электронов.

 Диффузионный ток дырок

, А/м²,                  (3.22а)

где D_p – коэффициент диффузии дырок с концентраций p.

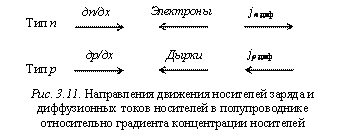
Диффузионный ток электронов совпадает с направлением вектора градиента концентрации электронов, а диффузионный ток дырок противоположен направлению вектора градиента концентрации дырок (рис. 3.11).

Между коэффициентами диффузии и подвижностями носителей заряда существует взаимосвязь, выражаемая соотношениями Эйнштейна. Коэф­фи­циент диф­­фузии D связан с подвижностью носителей за­ряда m со­отношением Эйнштейна.  Для электронов

, м²/сек                           (3.23а)

где k - постоянная Больцмана, Дж/К; Т – температура, К; q - заряд электрона, Кл; φ_т =kT/q– тепловой потенциал, В; μ_n– подвижность электронов, м²/В·c.

Соотношение Эйнштейна для дырок:

, м²/сек                           (3.23б)

где q - заряд дырки, Кл; μ_p– подвижность дырок, м²/В·c.

Представляет интерес расчет средней длины пробега неравно­вес­ных носителей заряда в течение их времени жизни. Длина пробега ха­ра­к­­те­ри­зу­ется так называемой диффузионной длиной носителей. Ди­ф­­фузионная длина L - это среднее расстояние, на которое но­си­­­­тели заряда перемеща­ют­ся за время жизни t. Значение L рас­счи­тывается по формуле

, м,                                                (3.24)

где D - коэффициент диффузии носителей заряда, м²/сек.

 Типичные значения диффузионной длины носителей за­­ряда в по­­лу­­проводниках составляют (0,2...3)×10^-6 м=(0,2...3) мкм. Чем мень­­­­­­ше примесей и дефектов в полупро­вод­нике, т. е. чем чи­ще по­­­­­­лупроводник, тем бо­ль­ше время жизни t, и, соответственно, боль­­­­­­ше диффузионная дли­на L не­рав­но­­весных носителей заряда.

Зависимость подвижности и коэффициента диффузии от типа носителей заряда и материала полупроводника. Из соотношений Эйнштейна (3.23) следует пропорциональная связь между коэффициентом диффузии носителей заряда и их подвижностью.

 Величина подвижности, и, следовательно, коэффициента диффузии зависят от материала полупроводника, в частности, от ширины его запрещенной зоны. В таблице 3.1 приведены значения коэффициентов диффузии и подвижностей для основных полупроводников.

Таблица 3.1
Полупроводник	Si	Ge	GaAs	In Sb
Ширина запрещенной зоны, ΔWg, эВ	1,12	0,66	1,43	0,18
Подвижность электронов, μn, м2/В·с	0,15	0,39	0,85	7,8
Коэффициент диффузии электронов, Dn, м2/c	0,0036	0,0029	0,01	0,91
Подвижность дырок, μp, м2/В·с	0,045	0,19	0,045	0,075
Коэффициент диффузии дырок, Dp, м2/c	0,0013	0,0012	0,0045	0,0017

Таким образом, в полупроводниках подвижность электронов, как правило, выше, чем подвижность дырок, а наиболее высокая подвижность электронов наблюдается в сложных полупроводниковых соединениях типа А³B^3.

Следует отметить, что диффузия носителей заряда происходит также при наличии в полупроводнике градиента температуры. В этом случае носители заряда, находящиеся в области с более высокой температурой будут иметь более высокую энергию. Поэтому возникает диффузия носителей заряда из нагретой области в холодную.