Емкость p-n перехода
 В
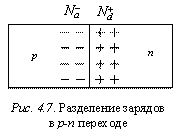
высокоомном обедненном слое p-n перехода по обе стороны от его границы существуют равные по
значению и противоположные по знаку объемные заряды: отрицательный в p –области, положительный
- в n-области. Эти заряды обусловлены
наличием ионов примесей
В
высокоомном обедненном слое p-n перехода по обе стороны от его границы существуют равные по
значению и противоположные по знаку объемные заряды: отрицательный в p –области, положительный
- в n-области. Эти заряды обусловлены
наличием ионов примесей ![]() и
и ![]() (рис. 4.7), а при подаче прямого смещения на переход – дополнительными
зарядами, возникшими в процессе инжекции неосновных
носителей заряда. В зависимости от приложенного напряжения изменяется толщина
обедненного слоя и, следовательно, значения зарядов Q. Это указывает на то, что p-n переход обладает электрической емкостью
(рис. 4.7), а при подаче прямого смещения на переход – дополнительными
зарядами, возникшими в процессе инжекции неосновных
носителей заряда. В зависимости от приложенного напряжения изменяется толщина
обедненного слоя и, следовательно, значения зарядов Q. Это указывает на то, что p-n переход обладает электрической емкостью ![]() , где U – контактная разность потенциалов
в p-n переходе. В общем случае емкость p-n перехода
складывается из двух составляющих:
, где U – контактная разность потенциалов
в p-n переходе. В общем случае емкость p-n перехода
складывается из двух составляющих:
С=Сбар+Сдф, (4.13)
где Сбар – барьерная емкость p-n перехода при подаче на него обратного напряжения Uобр; Сдф – диффузионная емкость, возникает при подаче на p-n переход прямого напряжения Uпр.
Емкость при обратном
напряжении. Обратносмещенный р-п переход характеризуется удельной барьерной емкостью ![]() , где S - площадь
перехода. Природа барьерной емкости связана с разделением зарядов в
обедненной области p-n перехода. Величина этого заряда в ступенчатом (резком) определяется соотношением
, где S - площадь
перехода. Природа барьерной емкости связана с разделением зарядов в
обедненной области p-n перехода. Величина этого заряда в ступенчатом (резком) определяется соотношением
![]() , (4.14)
, (4.14)
где Nd и Nа - концентрация примеси в n- и p- областях перехода.
Учитывая формулу (4.4) для расчета ширины обедненного слоя l, в которой значение jк заменено на jк +U,
![]() ,
,
для величины заряда получаем
![]() .
(4.15)
.
(4.15)
Проводя дифференцирование (4.15) по напряжению U, получим искомое соотношение для удельной барьерной емкости p-n перехода в виде
![]() . (4.16)
. (4.16)
Если p-n переход несимметричный, то есть концентрация легирующей примеси в одной из областей перехода значительно превышает концентрацию в другой области, то выражение для Сбар упрощается и принимает вид
![]() , (4.17)
, (4.17)
где N – концентрация примеси в высокоомной области p-n перехода
Для кремния
при N=1022 м-3 и
U=4 В получаем значение Сб
около 1,5×10-4 Ф/м2. При площади перехода S=10-
Зависимость емкости от напряжения называется вольт-фарадной характеристикой. Из соотношений (4.16) и (4.17) следует, что с ростом обратного смещения на p-n переходе барьерная емкость довольно быстро снижается. Это свойство используется при изготовлении конденсаторов переменной емкости с электрическим управлением величиной емкости, называемых варикапами.
Емкость при прямом напряжении. В данном случае существуют две физические причины, определяющие емкость p-n перехода. Первая из них – та же, что и для обратного напряжения: это изменение зарядов в обедненном слое. Вторая заключается в том, что с увеличением напряжения, приложенного к p-n переходу, возрастает концентрация инжектированных носителей в нейтральных областях вблизи границ перехода и, соответственно, значение накопленного заряда, обусловленного этими носителями. Следовательно, возрастает значение накопленного заряда Qдф, обусловленного этими носителями.
Величина диффузионной емкости рассчитывается из выражения
![]() ,
,
где Qдф=jτ; ![]() - прямой диффузионный
ток через p-n переход; τ
– время жизни носителей заряда.
- прямой диффузионный
ток через p-n переход; τ
– время жизни носителей заряда.
Дифференцируя выражение для диффузионной емкости, получим,
![]() .
(4.18)
.
(4.18)
Введем понятие дифференциального
сопротивления p-n перехода ![]() . Тогда выражение для диффузионной емкости приобретает вид
. Тогда выражение для диффузионной емкости приобретает вид
![]() .
(4.19)
.
(4.19)
 В
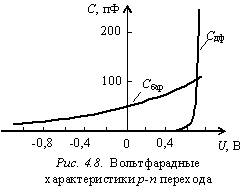
качестве примера на рис. 4.8 показана зависимость полной емкости p-n перехода
от напряжения для кремния.
В
качестве примера на рис. 4.8 показана зависимость полной емкости p-n перехода
от напряжения для кремния.
Барьерная емкость резкого p-n перехода Сбар уменьшается с ростом абсолютной величины обратного напряжения по закону (4.16). Диффузионная емкость Сдф увеличивается с ростом прямого напряжения по экспоненциальному закону (4.18). Поэтому диффузионная емкость меньше барьерной вплоть до напряжения отпирания p-n перехода (U<0,5…0,6 В), затем она резко увеличивается и, при U>0,6 В, начинает превышать барьерную емкость.
В полупроводниках можно создать также более сложные по физической структуре n-p-n и р-n-p, а также n-p-n-p и р-n-p-n переходы, позволяющие усиливать и переключать токи. Указанные переходы лежат в основе создания полупроводниковых приборов, называемых биполярными транзисторами и тиристорами.