Эффект Холла
Эффект, открытый американским физиком Эдвином Гербертом Холлом в 1879 году, заключается в явлении возникновения поперечной разности потенциалов в полупроводнике, по которому протекает электрический ток и существует магнитное поле Н, перпендикулярное направлению тока.
Физическая природа эффекта Холла заключается в том, что на движущийся носитель тока в магнитном поле с индукцией В действует сила Лоренца
, Н, (6.11)
где v –скорость носителя; q – его заряд.
Направление силы Лоренца определяется правилом левой руки. Если проводник n-типа проводимости, то электроны будут смещаться влево к внешней стороне пластины, заряжая её отрицательно (рис. 6.8).
В полупроводника p-типа проводимости при том же направлении тока сила Лоренца
будет смещать дырки в том же направлении. При этом левая внешняя сторона пластинки
зарядится положительно.
Если угол между вектором скорости носителей v и вектором магнитной индукции B равен 90о, то величина силы Лоренца рассчитывается по формуле
Fл=qvB, (6.12)
где v – средняя дрейфовая скорость носителей заряда, м/c.
Электрическое поле между поперечными гранями пластинки равно
, В/м,
(6.13)
где Uх » (0,6…1)·10-4 В - разность потенциалов между поперечными гранями пластинки, называемая эдс Холла; а – ширина пластинки.
Поле Ех действует на электроны с силой F=-qEх, направленной против силы Лоренца Fл. При выполнении условия Fл=F поперечное электрическое поле уравновешивает силу Лоренца и дальнейшее накопление электрических зарядов на боковых гранях пластины прекращается. Тогда из равенства qvB=qEх следует Eх=vB. Дрейфовая скорость носителей тока определяется из выражения
,
(6.14)
где j – плотность тока, А/м2, n – концентрация электронов, м-3,
Тогда выражение для поля Ех приобретает вид
.
(6.15)
Умножив обе части равенства (6.15) на ширину пластинки а, получаем формулу для эдс Холла
, В. (6.16)
Формула (6.16) обычно записывается в виде
,
(6.17)
где 
– коэффициент Холла, м3/Кл.
С учетом разброса средней скорости дрейфа электронов в полупроводнике значение коэффициента Холла определяется из выражения
,
(6.18)
где А=1,18 для полупроводников с преимущественным рассеянием носителей заряда на тепловых колебаниях кристаллической решетки; А=1,93 при рассеянии на ионизированных примесях.
Для дырочных полупроводников коэффициент Холла рассчитывается по формуле
,
(6.19)
где q и p –заряд и концентрация дырок, соответственно.
При смешенной электронно-дырочной проводимости величина коэффициента Холла рассчитывается по формуле
,
(6.20)
где μn и μp – подвижности электронов и дырок, соответственно.
Из формулы (6.20) следует, что в собственных полупроводниках при выполнении условия ni=pi значение коэффициента Холла равно
.
(6.21)
6.2.2. Преобразователи Холла
Это гальваномагнитные полупроводниковые приборы, основанные на использовании эффекта Холла.
ЭДС преобразователя Холла конечной длины рассчитывается по формуле
, (6.22)
|
|
где J – ток через преобразователь, А; δ –
толщина преобразователя, м; l –
длина преобразователя; а – ширина преобразователя; 
- поправочная функция,
график которой приведен на рис. 6.9.
Материалом для преобразователя Холла служит монокристаллическая пластинка из Ge или InSb. Эти материалы характеризуются высокой подвижностью электронов. Также используются тонкие пленки с толщиной δ=0,01…0,1 мкм, нанесенные на диэлектрическую подложку методом испарения в вакууме. Материалами служат HgSe, HgTe, сплавы HgSe-HgTe, в которых подвижность электронов достигает значения 1 м2/ (В·с). Конструкция преобразователя Холла показана на рис. 6.10. Для устранения неэквипотенциальности выходных электродов 2-2 в схеме подключения преобразователя предусмотрен переменный резистор Rк. Предельная частота работы преобразователей Холла достигает 10…100 МГц.
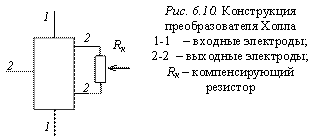
Поскольку величина ЭДС Холла Uх пропорциональна произведению B·J, то преобразователи Холла применяют для измерения магнитных полей и токов, в перемножающих аналоговых устройствах, в схемах модуляторов и детекторов, в качестве анализаторов спектра сигналов.
Основными параметрами преобразователей Холла являются следующие.
1. Входное сопротивление 
– это сопротивление
между входными электродами (1-1 на рис. 6.10), Ом.
2. Выходное сопротивление, Rвых, - сопротивление между выходными электродами, Ом.
3. КПД преобразователя Холла, 
, - отношение отдаваемой, Pн, и подводимой мощности, Pвх.
4. Коэффициент передачи, 
, - это отношение напряженности поля ЭДС Холла, Ех, к напряженности поля Евх между входными электродами.
5. Максимально допустимый ток через преобразователь, 
, где а
–ширина преобразователя, м; α – коэффициент теплоотдачи с поверхности
преобразователя, Вт/(м2К); ΔТ»50 К – температура перегрева преобразователя; δ – толщина
преобразователя, м; r
- удельное электросопротивление полупроводника, Ом·м.
6. Максимальная ЭДС Холла, Uх max=RxBImax, - значение ЭДС Холла при заданной индукции магнитного поля B при протекании через датчик максимально допустимого тока Imax, В.
7. Вольтовая чувствительность 
, В/Т .
6.2.3. Биполярный магнитотранзистор
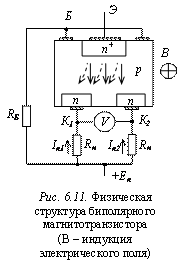Это
транзистор, в котором используется зависимость его характеристик и параметров
от магнитного поля. Для увеличения чувствительности к магнитному полю
биполярные транзисторы выполняют с двумя коллекторными переходами (рис.6.11). Поток
магнитной индукции B отклоняет носители тока (электроны) от одного коллектора к
другому. Между коллекторами возникает разность потенциалов
U=(Iк1 – Ir2)Rн.
Биполярные магнитотранзисторы имеют вольтовую чувствительность в 100…1000 раз больше магнитной чувствительности преобразователя Холла.
