Подвижность. Дрейф носителей заряда

Если в полупроводнике создано электрическое поле величины Е, то помимо хаотического появляется направленное перемещение носителей заряда, называемое дрейфом. Скорость дрейфа, v_др, – это скорость, направленная вдоль вектора напряженности электрического поля, усредненная по всем носителям заряда одного знака (электронами или дырками).

Оценить среднюю скорость дрейфа можно исходя из формулы v_др=a t_п, где а – ускорение, приобретаемое электроном между столкновениями. Среднее ускорение электрона можно рассчитать, используя второй закон Ньютона

 ,

где qE=F – сила, действующая на электрон со стороны поля.

Подставив это выражение в формулу для скорости дрейфа, получаем

.                                           (3.1)

В формуле (3.1)  величина называется подвижностью носителей заряда. Таким образом, под­ви­­ж­ность носителей заряда обратно про­пор­циональна эф­фек­ти­­в­­ной массе носителей m и прямо про­по­р­ци­ональна времени свободного пробега t_п.

Поскольку скорость дрейфа v_др=μЕ, то значение подвижности можно рассчитать по формуле

, м²/В·с.                                       (3.2)

Иначе говоря, подвижность носителей заряда – это скорость дрейфа, приобретаемая свободными носителями в электрическом поле напряженности Е=1 В/м.

Оценка величины подвижности электрона μ в кристаллической решетке по формуле (3.1) дает следующее значение:

м²/В·с.

Поскольку в полу­про­водниках су­ще­ст­ву­­­ют два вида носи­­те­лей заряда с различными эффективными мас­­­­сами, то раз­личают под­вижность электронов m_n и подвиж­ность дырок m_p. Под­виж­ность электронов в кремнии по различным данным со­ста­в­ля­ет  (0,14...0,19) м²/(В×с), а в арсениде галлия – (0,93...1,1) м²/(В×с). Под­ви­ж­ность дырок ока­­зывается значительно меньшей и ра­в­ной (0,04...0,05) м²/(В×с) для кремния и германия и 0,045 м²/(В×с) для арсенида галлия, что объясняется меньшим временем свободного пробега ды­рок в этих полупроводниковых ма­териалах.

Температурная зависимость величины подвижности но­сите­лей заряда в полупроводниках определяется механизмами рас­се­я­ния но­сителей заряда.

В слабых электрических полях дрейфовая скорость значительно меньше средней скорости теплового хаотического движения. Длина свободного пробега определяется в основном рассеянием свободных носителей на колеблющихся атомах полупроводника (фононах) и ионизированных атомах при­месей. Фононное рассеяние преобладает при малых концентрациях при­месей (10²⁰...10²³ м^-3), в этом случае длина свободного пробега, следо­ва­тельно и подвижность, уменьшаются с ростом температуры (рис. 3.1, а).

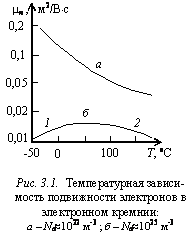Подвижность носителей заряда в полупроводнике становится значи­тель­но меньшей при высокой концентрации примесей, 10²⁴...10²⁵ м^-3. В этом случае при сравнительно низких температурах преоб­ла­дает рас­се­я­ние носителей за­ряда на примесях, находящихся в ионизи­ро­ван­ном или ней­т­раль­ном состоянии. При нагреве полупроводника вследствие увеличения тепловой скорости электронов и уменьшения их времени взаимодействия с ионами, подвижность но­си­­телей заряда m_и  ра­стет с тем­пературой по закону m_и~T^3/2/N_и, где N_и - кон­це­н­т­ра­ция ионизированных примесей (доноров или ак­­­цепторов). При высоких температурах преобладает рас­се­яние но­си­те­лей заряда на тепловых колебаниях атомов или ио­нов кри­стал­ли­чес­кой ре­ше­тки полупроводника. При этом по­­­д­ви­ж­ность m_т уме­нь­­ша­е­тся с ростом температуры по закону m_т ~T ^-3/2.

График зависимости m=f(T) в сильно легированом полупроводнике представлен на рис. 3.1, б. Видно, что температурная зависимость по­д­­вижности носителей заряда в при­мес­ном полупроводнике со­с­то­ит из двух участков. Участок 1 ха­ра­кте­рен для низких тем­пе­ра­тур, ко­гда пре­обладает рассеяние на ио­ни­зи­ро­ванных примесях; на уча­с­­т­ке 2 по­д­вижность но­си­те­лей умень­ша­­е­т­ся вследствие рассеяния на теп­ло­вых колебаниях ато­мов и ионов.

 Результирующая подвижность m определяется с помощью соотношения

.                                         (3.3)

Подвижность и дрейфовая скорость носителей заряда за­ви­­сят не только от темпе­ра­ту­ры, но и от напряженности элек­три­че­с­­­­ко­­го по­ля в по­лу­про­во­д­ни­ке.

В слабых электрических полях v_др<<v_т, тогда полная средняя скорость не зависит от напряженности поля Е и подвижность m=m_o постоян­на. Дополнительная, приобретаемая электронами на длине свободного пробега, энергия много меньше kT, она теряется при рассеянии на возбуждение низкочастотных акустических фононов (п. 1.5.7).

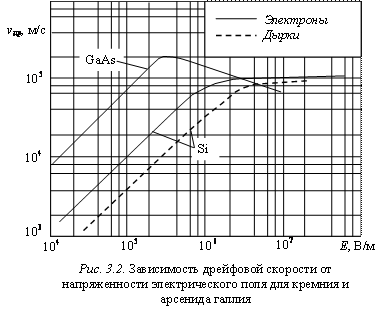
С ростом напряженности электрического поля скорость дрейфа электронов возрастает (рис. 3.2), приобретаемая электронами энергия увеличивается и начинает превышать потери при рассеянии, поскольку энергия возбуждаемых акустических фононов по-прежнему мала по сравнению с kT. Это вытекает из условия сохранения импульса - импульс возбуждаемого фонона должен быть равен изменению импульса электрона. Однако импульс акустического фонона p_фон== =(h/v_фон)f_фон с энергией W_фонkT значительно превышает импульс электрона из-за невысокой скорости фонона v_фон5·10³ м/с и энергия электрона не может быть передана фононам с такой энергией.

Вследствие увеличения средней скорости электронов уменьшается время свободного пробега t_п электрона между двумя столкновениями и, согласно соотношению (3.1), подвижность уменьшается.  Известно, что подвижность снижается на 10%, когда напряженность электрического поля достигает критического значения E_кр=1,4v_фон/m₀, где m₀ - значение подвижности в слабом электрическом поле. Таким образом, значение критического поля обратно пропорционально величине подвижности носителей заряда в конкретном полупроводниковом материале. В кремнии для электронов E_кр=7,5·10⁴ В/м, а для дырок E_кр=2·10⁵ В/м при Т=300 К. Следовательно, в кремнии величина критического поля для дырок примерно в 2,5 раза выше, чем для электронов, характеризующихся более высокой подвижностью.

 Величина подвижности носителей заряда, в свою очередь, зависит от напряженности электрического поля. При E>>v_фон/m₀ подвижность уменьшается с ростом напряженности поля Е по закону m~1/, а дрейфовая скорость увеличивается: v_др~.

В сильных электрических полях (Е=10⁶...10⁷ В/м), когда скорость дрейфа приближается к средней тепловой скорости, средняя энергия электронов становится достаточной для возбуждения оптических фононов. В отличие от акустических оптические фононы при сравнительно небольших импульсах того же порядка что и у электрона, обладают большими энергиями (2...3)kТ при Т=300 K. В процессе рассеяния электроны отдают почти всю свою кинетическую энергию на образование фононов, поскольку как только она достигает величины W_{фон. опт}, возбуждается фонон и энергия электрона снижается. В этих условиях время свободного пробега t_п и подвижность обратно пропорциональны напряженности электрического поля: m~1/Е, а дрейфовая скорость перестает зависеть от Е и достигает предельного значения - скорости насыщения v_нас. В кремнии при Т=300 К для электронов v_нас=10⁵ м/c, а для дырок v_нас=8×10⁴ м/c.

Скорость насыщения v_нас является важнейшим электрофизическим параметром полупроводника. При Т=300 К она имеет значение близкое к тепловой скорости, однако в отличие от последней v_нас может уменьшаться с ростом температуры. Например, в кремнии n-типа в диапазоне температур от минус 50 до +120 ^оС скорость насыщения v_нас уменьшается в диапазоне (1,1...0,8)×10⁵, а тепловая скорость v_т – возрастает в диапазоне (1,7...2)×10⁵ м/с.

Для кремния и германия  зависимость дрейфовой скорости от напряженности электрического поля может быть аппроксимирована формулой

,                                              (3.4)

где m₀ - значение подвижности в слабом электрическом поле.

Таким образом, дрейфовая скорость в полупроводниках возрастает с ростом напряженности электрического поля, достигая своего максимального значения – скорости насыщения, близкого к тепловой скорости.

Зависимость подвижности носителей заряда (электронов или дырок) от напряженности электрического поля в кремнии аппроксимируется выражением

.                                        (3.5)

Подвижность носителей заряда в средних и сильных электрических полях уменьшается с ростом напряженности электрического поля.

Дрейфовый ток

Создание в од­­но­­­ро­дном полупроводнике электрического поля с напря­жен­но­с­тью E, в результате подключения внешнего ис­точ­ника ЭДС или тока, при­во­­дит к по­явлению дре­й­фа носителей тока (электронов и ды­рок).

Поскольку знаки зарядов электронов и дырок противоположны, то носители дрейфуют со скорос­тью v_др в про­ти­воположных на­правлениях в со­от­ве­­тствии с си­ла­ми,  дей­с­т­ву­ю­щи­ми со сто­ро­ны эле­к­т­ри­ческого поля. Поэтому соответствующие дрейфовые токи складываются, как показано на рис. 3.3.

 Плот­ность дрейфового тока j_др в соб­ст­­вен­ном по­лу­про­вод­нике складывается из плотностей токов эле­к­т­­ро­нов j_{n др} и ды­рок j_{p др} и определяется из выра­же­ни­я

j_др= j_{n др+} j_{p др=}(qn_iv_{n др}+qp_iv_{p др})= qn_i(m_n+m_p)E, А/м²,            (3.6)

где q - заряды; n_i=p_i- концентрации; v_{n др} и v_{p др} -  скорости дрейфа; m_n и m_p - подвижности эле­к­т­ро­нов и дырок.

В примесных полупроводниках общая плотность дрейфового тока электронов и дырок

j_др= j_{n др+} j_{p др=q}(nm_n+pm_p)E, А/м²,                              (3.7)

В рабочей области температур плотность дрейфового то­ка определяется, преимущественно, ос­но­в­­­ными носителями тока и рассчитывается по формулам j_{n др=qnnmnE} и j_{p др=qppmpE}, где n_n и p_p - концентрации основных но­си­те­­лей тока в электронном и ды­­рочном полу­про­вод­ни­ках.